Thirza Dado

PhD Candidate at the Neural Coding Lab who studies how the world is represented by the brain using synthesized reality.

Tutorial on hyperaligning and decoding of the brain

2022, 22 January

HYperrealistic reconstruction of PERceived faces from fMRI data

Written by Thirza Dado & Umut Güçlü.

Top Stimuli (top row) and their reconstructions from brain data (bottom row).

Neural decoding seeks to find what information about a perceived external stimulus is present in the corresponding brain response. In particular, the original stimulus can be reconstructed based on brain data alone. This study resulted in the most accurate reconstructions of face perception to date by decoding the brain recordings of two individual participants separately. To get even closer, we repeated this approach with the averaged brain responses.

Here, we show you how we did it.

HYPER

In the original paper, two participants in the brain scanner were presented with face stimuli that elicited specific functional responses in their brains. This experiment resulted in a (faces, responses) dataset that taught a decoder to map brain responses to the corresponding faces. This trained decoder could now transform unseen (held-out) brain data back into the perceived stimuli. The model was called HYPER (HYperrealistic reconstruction of PERception).

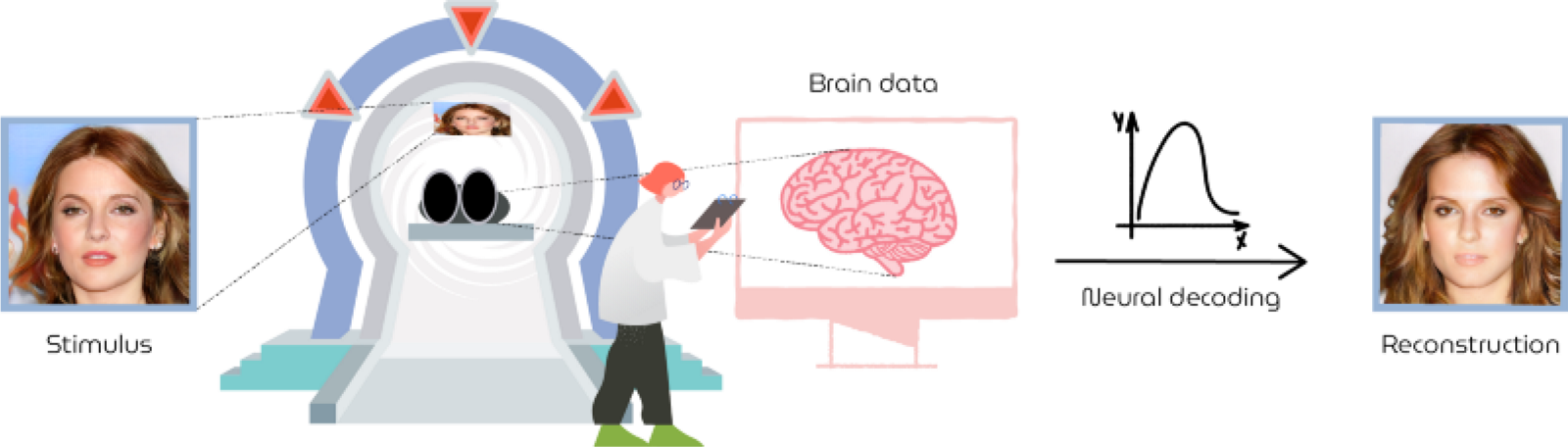Experiment The face stimulus was presented to the participant in the MRI scanner that recorded the corresponding neural responses. Neural decoding of these responses then reconstructed what the participant was originally seeing.

The secret ingredient was the following: the face stimuli were artificially synthesized by the generator network of a progressively grown GAN for faces from randomly sampled latent vectors; the people in the presented images did not really exist. As such, the latents underlying these faces were known (because they were used for generation in the first place) whereas those of real face images can never be directly accessed - only approximated which entails information loss. Note that these results are legitimate reconstructions of visual perception regardless of the nature of the stimuli themselves.

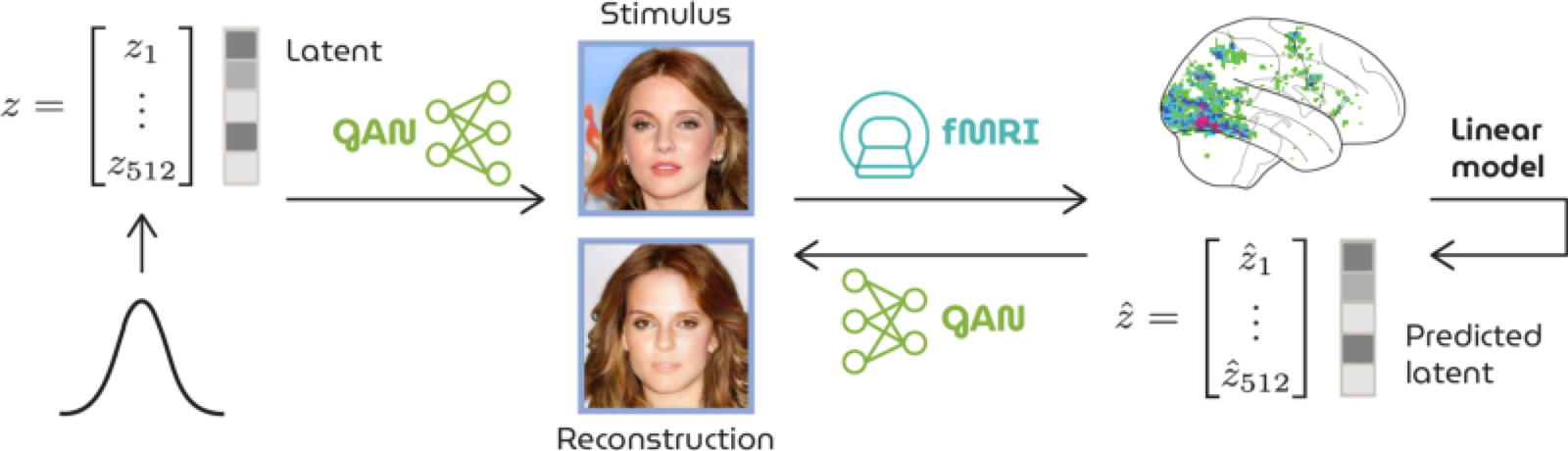Pipeline Schematic workflow of HYPER. A latent is fed to the GAN to generate a face image that is presented to a participant in the MRI scanner. From the recorded brain response to this stimulus, we predict a latent that is also fed to the GAN for (re-)generation.

The high resemblance indicates a linear relationship between latents and brain recordings. Simply put, latents and brains effectively captured the same defining stimulus features (e.g., age, gender, hair color, pose) so that latents could be predicted as a linear combination of the brain data and fed to the generator for (re-)generation of what was perceived.

Hyperalignment (brain remix)

The original study trained a separate decoder for each individual participant. To get even closer to the external stimulus, we can capture the shared neural information across participants by applying an additional preprocessing step to the brain data. This step involves aligning and reslicing the functional brain responses with hyperalignment - a remixing process that iteratively maps brain data of multiple participants to a common functional space. Note that we are working in the functional domain which is about brain function rather than the topography in the anatomical domain. The responses of different brains are now comparable in function and the average brain response per stimulus can be taken to train one general decoder.

All the stimulus-reconstruction pairs in this post result from HYPER with hyperaligned and averaged data.

Recon1 Stimuli (top row) and their reconstructions from brain data (bottom row).

Recon2 Stimuli (top row) and their reconstructions from brain data (bottom row).

Tutorial

Hyperalignment can be implemented using PyMVPA:

!apt-get install swig
!pip install -U pymvpa2
import mvpa2.datasets
import mvpa2.algorithms.hyperalignment
import numpy as np
import pickle

def hyperalignment(a, b):    
    x = [a, b]    
    dataset = [mvpa2.datasets.Dataset(x_) for x_ in x]    
    hyperalignment = mvpa2.algorithms.hyperalignment.Hyperalignment()(dataset)    
    y = [hyperalignment[j].forward(dataset[j]).samples for j in range(len(dataset))]    
    return (y[0] + y[1]) / 2

Load in the data (publicly accessible in Google Drive). The test and training set consist of 36 and 1050 trials of 4096 (flattened) voxel responses, respectively. Concatenate the test and training data before hyperalignment.

with open("yourpath/data_1.dat", 'rb') as f:
    X_tr1, _, X_te1, _ = pickle.load(f)
with open("yourpath/data_2.dat", 'rb') as f:
    X_tr2, _, X_te2, _ = pickle.load(f)
X_1 = np.array(X_te1 + X_tr1)
X_2 = np.array(X_te2 + X_tr2)
X_hyperaligned = hyperalignment(X_1, X_2)

Train a neural decoder to predict latents from brain data. This decoder is implemented in MXNet. Let’s import the required libraries.

!pip install mxnet-cu101
from __future__ import annotations
import os
from typing import Tuple, Union
import matplotlib.pyplot as plt
import mxnet as mx
from mxnet import autograd, gluon, nd, symbol
from mxnet.gluon.nn import Conv2D, Dense, HybridBlock,       
    HybridSequential, LeakyReLU
from mxnet.gluon.parameter import Parameter
from mxnet.initializer import Zero
from mxnet.io import NDArrayIter
from PIL import Image
from scipy.stats import zscore

Below you can find a MXNet implementation of the PGGAN generator. It takes a 512-dimensional latent and transforms it into a 1024 ×1024 RGB image.

class Pixelnorm(HybridBlock):
    def __init__(self, epsilon: float = 1e-8) -> None:
        super(Pixelnorm, self).__init__()
        self.eps = epsilon
    def hybrid_forward(self, F, x) -> nd:
        return x * F.rsqrt(F.mean(F.square(x), 1, True) + self.eps)

class Bias(HybridBlock):
    def __init__(self, shape: Tuple) -> None:
        super(Bias, self).__init__()
        self.shape = shape
        with self.name_scope():
            self.b = self.params.get("b", init=Zero(), shape=shape)
    def hybrid_forward(self, F, x, b) -> nd:
        return F.broadcast_add(x, b[None, :, None, None])

class Block(HybridSequential):
    def __init__(self, channels: int, in_channels: int) -> None:
        super(Block, self).__init__()
        self.channels = channels
        self.in_channels = in_channels
        with self.name_scope():
            self.add(Conv2D(channels, 3, padding=1, in_channels=in_channels))
            self.add(LeakyReLU(0.2))
            self.add(Pixelnorm())
            self.add(Conv2D(channels, 3, padding=1, in_channels=channels))
            self.add(LeakyReLU(0.2))
            self.add(Pixelnorm())
    def hybrid_forward(self, F, x) -> nd:
        x = F.repeat(x, 2, 2)
        x = F.repeat(x, 2, 3)
        for i in range(len(self)):
            x = self[i](x)
        return x

class Generator(HybridSequential):
    def __init__(self) -> None:
        super(Generator, self).__init__()
        with self.name_scope():
            self.add(Pixelnorm())
            self.add(Dense(8192, use_bias=False, in_units=512))
            self.add(Bias((512,)))
            self.add(LeakyReLU(0.2))
            self.add(Pixelnorm())
            self.add(Conv2D(512, 3, padding=1, in_channels=512))
            self.add(LeakyReLU(0.2))
            self.add(Pixelnorm())
            self.add(Block(512, 512))
            self.add(Block(512, 512))
            self.add(Block(512, 512))
            self.add(Block(256, 512))
            self.add(Block(128, 256))
            self.add(Block(64, 128))
            self.add(Block(32, 64))
            self.add(Block(16, 32))
            self.add(Conv2D(3, 1, in_channels=16))
    def hybrid_forward(self, F: Union(nd, symbol), x: nd, layer: int) -> nd:
        x = F.Reshape(self[1](self[0](x)), (-1, 512, 4, 4))
        for i in range(2, len(self)):
            x = self[i](x)
            if i == layer + 7:
                return x
        return x

A dense (decoding) layer then transforms the 4096-dimensional functional responses into 512-dimensional latents. Only train the weights of this layer and keep the generator weights fixed.

class Linear(HybridSequential):
    def __init__(self, n_in, n_out):
        super(Linear, self).__init__()
        with self.name_scope():
            self.add(Dense(n_out, in_units=n_in))

Before training, all data have to be transformed to be of type NDArray (make sure to also store on GPU if you have access). The weight parameters of the generator (MXNet) can be found on Drive. Note that we are using gradient descent to fit the weights of the dense layer whereas ordinary least squares would yield a similar solution. However, the current setup allows you to experiment and try different things to make more sophisticated models (e.g., predict intermediate layer activations of PGGAN and include this in your loss function).

# Set parameters.
batch_size = 30
max_epoch = 1500
n_lat = 512
n_vox = 4096

# Make dataset to take batches from during training.
def load_dataset(t, x, batch_size):
    return NDArrayIter({ "x": nd.stack(*x, axis=0) }, { "t": nd.stack(*t, axis=0) }, batch_size, True)

# Latents.
with open("yourpath/data_1.dat", 'rb') as f:
    _, T_tr, _, T_te = pickle.load(f)

# Z-score the brain data.
X_te = zscore(X_hyperaligned[:36])
X_tr = zscore(X_hyperaligned[36:])
train = load_dataset(nd.array(T_tr), nd.array(X_tr), batch_size)
test =  load_dataset(nd.array(T_te), nd.array(X_te), batch_size=36)

# Initialize generator.
generator = Generator()
generator.load_parameters("yourpath/generator.params")
mean_squared_error = gluon.loss.L2Loss()

# Initialize linear model.
vox_to_lat = Linear(n_vox, n_lat)
vox_to_lat.initialize()
trainer = gluon.Trainer(vox_to_lat.collect_params(), "Adam", {"learning_rate": 0.00001, "wd": 0.01})

# Training.
epoch = 0
results_tr = []
results_te = []
while epoch < max_epoch:
    train.reset()
    test.reset()
    loss_tr = 0
    loss_te = 0
    count = 0
    for batch_tr in train:
        with autograd.record():
            lat_Y = vox_to_lat(batch_tr.data[0])
            loss = mean_squared_error(lat_Y, batch_tr.label[0])
        loss.backward()
        trainer.step(batch_size)
        loss_tr += loss.mean().asnumpy()
        count += 1
    for batch_te in test:
        lat_Y = vox_to_lat(batch_te.data[0])
        loss = mean_squared_error(lat_Y, batch_te.label[0])
        loss_te += loss.mean().asnumpy()
    loss_tr_normalized = loss_tr / count
    results_tr.append(loss_tr_normalized)
    results_te.append(loss_te)
    epoch += 1
    print("Epoch %i: %.4f / %.4f" % (epoch, loss_tr_normalized, loss_te))
plt.figure()
plt.plot(np.linspace(0, epoch, epoch), results_tr)
plt.plot(np.linspace(0, epoch, epoch), results_te)
plt.show()

After training, reconstruct faces from the test set responses. Note that the test data is not used for training (you only computed the test loss per epoch for plotting purposes) such that the model never encountered this brain data before.

# Testing and reconstructing
lat_Y = vox_to_lat(nd.array(X_te))
dir = "yourpath/reconstructions"
if not os.path.exists(dir):
    os.mkdir(dir)
for i, latent in enumerate(lat_Y):
    face = generator(latent[None], 9).asnumpy()
    face = np.clip(np.rint(127.5 * face + 127.5), 0.0, 255.0)
    face = face.astype("uint8").transpose(0, 2, 3, 1)
    Image.fromarray(face[0], 'RGB').save(dir + "/%d.png" % i)

In the end, one decoding model was trained on averaged functional neural responses which resulted in face reconstructions spectacularly analogous to the originally perceived faces. This raises the question of how close neural decoding can get to objective reality if we average the brain data of an even larger pool of eyewitnesses.

That’s all folks!

Recon3

Recon4 Stimuli (top row) and their reconstructions from brain data (bottom row).

Dado, T., Güçlütürk, Y., Ambrogioni, L. et al. Hyperrealistic neural decoding for reconstructing faces from fMRI activations via the GAN latent space. Sci Rep 12, 141 (2022). https://doi.org/10.1038/s41598-021-03938-w

2023

Back to top ↑

2022

Back to top ↑