Get more from less: Differential neural decoding for effective reconstruction of perceived naturalistic stimuli from noisy and scarce neural data
Thirza Dado & Umut Güçlü
Proceedings of the Annual Meeting of the Cognitive Science Society 2024
06 May 2024
📝 Full paper
🪧 Poster
Abstract
Decoding naturalistic stimuli from neural recordings is a significant challenge in systems neuroscience, primarily due to the high-dimensional and nonlinear nature of stimulus-response interactions, and is further exacerbated by the limited availability and noisiness of neural data. While contemporary approaches that incorporate generative models, such as Generative Adversarial Networks (GANs), attempt to address these issues by mapping neural responses to latent representations, they do not fully overcome these obstacles. In this work, we present a novel paradigm of differential neural decoding (**dicoding**) that focuses on the relative changes in response patterns, which not only expands the neural training data quadratically but also inherently denoises it. To determine the corresponding stimulus changes, this method leverages the Euclidean and feature-disentangled properties of the underlying latents through vector arithmetic. As such, we not only effectively exploit the latent space but also achieve semantically meaningful latent offsets in the context of the stimuli, resulting in improved sample efficiency. We trained a decoder to predict changes in latent vectors based on the corresponding changes in neural responses. The absolute latent vector itself was derived by vector addition of the predicted latent change (indicative of stimulus shift) to a reference latent, which was fed to the generator for the reconstruction of the perceived stimulus. Our results show that this geometrically principled approach facilitates more effective reconstruction of naturalistic stimuli from noisy and limited neural data.
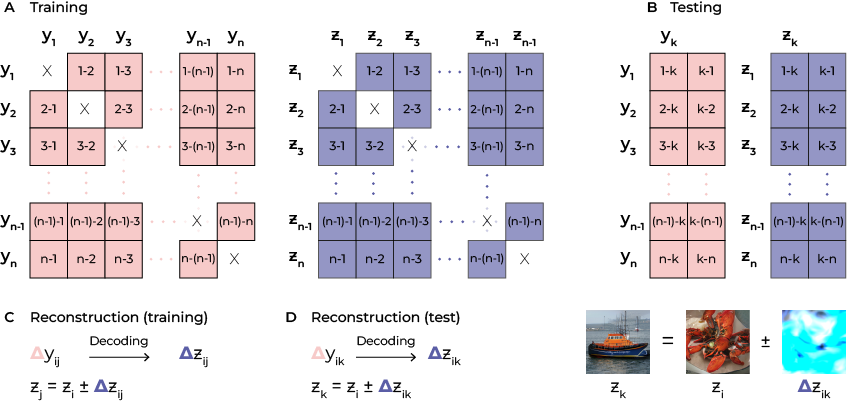
The training set (A) and test set (B) are constructed by taking the relative differences between pairs of examples. The stimulus itself can be reconstructed (C, D) by adding the predictive relative difference from brain activity to the known reference latent.
